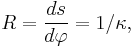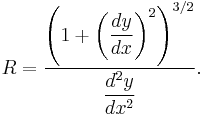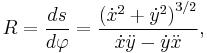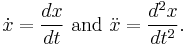Radius of curvature (mathematics)

In geometry, the radius of curvature, R, of a curve at a point is a measure of the radius of the circular arc which best approximates the curve at that point. It is the inverse of the curvature.

In the case of a space curve, the radius of curvature is the length of the curvature vector.

In the case of a plane curve, then it is the absolute value of

$R = \frac{ds}{d\varphi} = 1/\kappa,$

where s is the arc length from a fixed point on the curve, φ is the tangential angle and 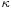$\scriptstyle\kappa$ is the signed curvature.

If the curve is given in Cartesian coordinates then the radius of curvature is (assuming the curve is differentiable up to order 2):

$R = \frac { \left(1 %2B \left(\dfrac{dy}{dx}\right)^2\right)^{3/2}}{\dfrac {d^2y}{dx^2}}.$

If the curve is given parametrically with parameter t then the radius of curvature is

$R = \frac{ds}{d\varphi} = \frac {\big({\dot{x}^2 %2B \dot{y}^2}\big)^{3/2}}{\dot {x}\ddot{y} - \dot{y}\ddot{x}},$

where

$\dot{x} = \frac{dx}{dt}\text{ and }\ddot{x} = \frac{d^2x}{dt^2}.$

References

do Carmo, Manfredo (1976). Differential Geometry of Curves and Surfaces. ISBN 0-13-212589-7.

Radius of curvature (mathematics)

See also

References